我就廢話不多說了，大家還是直接看代碼吧~

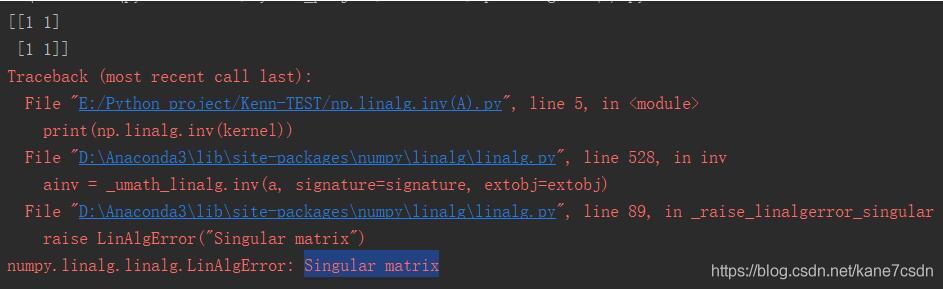
import numpy as np kernel = np.array([1, 1, 1, 2]).reshape((2, 2))print(kernel)print(np.linalg.inv(kernel))

注意，Singular matrix奇異矩陣不可求逆

補充：python+numpy中矩陣的逆和偽逆的區(qū)別

對于矩陣A，如果存在一個矩陣B，使得AB=BA=E，其中E為與A,B同維數(shù)的單位陣，就稱A為可逆矩陣（或者稱A可逆），并稱B是A的逆矩陣，簡稱逆陣。（此時的逆稱為凱利逆）

矩陣A可逆的充分必要條件是|A|≠0。

偽逆矩陣是逆矩陣的廣義形式。由于奇異矩陣或非方陣的矩陣不存在逆矩陣，但可以用函數(shù)pinv(A)求其偽逆矩陣。

基本語法為X=pinv(A),X=pinv(A,tol),其中tol為誤差,pinv為pseudo-inverse的縮寫：max(size(A))*norm(A)*eps。

函數(shù)返回一個與A的轉(zhuǎn)置矩陣A’ 同型的矩陣X，并且滿足：AXA=A,XAX=X.此時，稱矩陣X為矩陣A的偽逆，也稱為廣義逆矩陣。

pinv(A)具有inv(A)的部分特性，但不與inv(A)完全等同。

如果A為非奇異方陣，pinv(A)=inv(A)，但卻會耗費大量的計算時間，相比較而言，inv(A)花費更少的時間。

代碼如下：

import numpy as npa = np.array([[1, 2], [3, 4]]) # 初始化一個非奇異矩陣(數(shù)組)print(np.linalg.inv(a)) # 對應(yīng)于MATLAB中 inv() 函數(shù)# 矩陣對象可以通過 .I 求逆,但必須先使用matirx轉(zhuǎn)化A = np.matrix(a)print(A.I)2.矩陣求偽逆

import numpy as np# 定義一個奇異陣 AA = np.zeros((4, 4))A[0, -1] = 1A[-1, 0] = -1A = np.matrix(A)print(A)# print(A.I) 將報錯，矩陣 A 為奇異矩陣，不可逆print(np.linalg.pinv(A)) # 求矩陣 A 的偽逆（廣義逆矩陣），對應(yīng)于MATLAB中 pinv() 函數(shù)

這就是矩陣的逆和偽逆的區(qū)別

截至2020/10/4，matrix函數(shù)還可以使用，但已經(jīng)過時，應(yīng)該是mat函數(shù)這種。

以上為個人經(jīng)驗，希望能給大家一個參考，也希望大家多多支持好吧啦網(wǎng)。如有錯誤或未考慮完全的地方，望不吝賜教。