使用python實現時間序列白噪聲檢驗方式
白噪聲檢驗也稱為純隨機性檢驗, 當數據是純隨機數據時,再對數據進行分析就沒有任何意義了, 所以拿到數據后最好對數據進行一個純隨機性檢驗
acorr_ljungbox(x, lags=None, boxpierce=False) # 數據的純隨機性檢驗函數
lags為延遲期數,如果為整數,則是包含在內的延遲期數,如果是一個列表或數組,那么所有時滯都包含在列表中最大的時滯中
boxpierce為True時表示除開返回LB統計量還會返回Box和Pierce的Q統計量
返回值:
lbvalue:測試的統計量
pvalue:基于卡方分布的p統計量
bpvalue:((optionsal), float or array) ? 基于 Box-Pierce 的檢驗的p統計量
bppvalue:((optional), float or array) ? 基于卡方分布下的Box-Pierce檢驗的p統計量
代碼實現:
from statsmodels.stats.diagnostic import acorr_ljungboxacorr_ljungbox(b.salesVolume, lags = [6, 12],boxpierce=True)
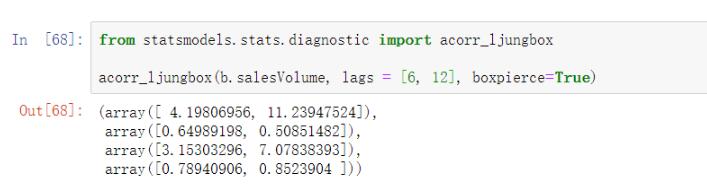
由輸出結果可以看到,不管是使用哪個統計量,p值都很大,所以該數據無法拒絕原假設,即認為該數據是純隨機數據
補充知識:用python實現時間序列單位根檢驗
在時間序列的建模中,需要先對數據進行平穩性檢驗,常用的有DF檢驗、ADF檢驗和PP檢驗,文章實例ADF檢驗
注:檢驗的P值是只在一個假設檢驗問題中,利用樣本觀測值能夠作出拒絕原假設的最小顯著性水平。
如果a >= p, 則在顯著性水平a 下拒絕H0
如果a < p,則在顯著性水平a下接受H0
實現方法一:
from arch.unitroot import ADFADF(data)

ADF檢驗的原假設是不平穩,這里P值近似為0 , 所以拒絕原假設,認為序列平穩。
from statsmodels.stats.diagnostic import unitroot_adfunitroot_adf(b.salesVolume)
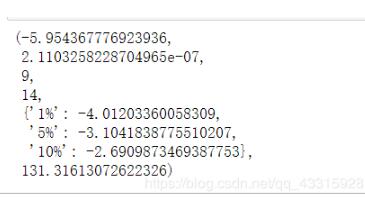
這里包含了檢驗值、p-value、滯后階數、自由度等信息。我們看到了檢驗統計量為?5.954367776923936,小于1%的臨界值-4.01203360058309,,即p值遠小于0.01,因此我們拒絕原假設,認為該時間序列是平穩的。(這里原假設是存在單位根,即時間序列為非平穩的。)
以上這篇使用python實現時間序列白噪聲檢驗方式就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。
相關文章:
 網公網安備
網公網安備