Python要求O(n)復雜度求無序列表中第K的大元素實例
昨天面試上來就是一個算法,平時基本的算法還行,結果變個法就不會了。。。感覺應該刷一波Leecode冷靜下。。。今天抽空看下。
題目就是要求O(n)復雜度求無序列表中第K的大元素
如果沒有復雜度的限制很簡單。。。加了O(n)復雜度確實有點蒙
雖然當時面試官說思路對了,但是還是沒搞出來,最后面試官提示用快排的思想
主要還是設立一個flag,列表中小于flag的組成左列表,大于等于flag的組成右列表,主要是不需要在對兩側列表在進行排序了,只需要生成左右列表就行,所以可以實現復雜度O(n)。
舉個例子說明下步驟,比如有列表test_list=[6,5,4,3,2,1],找出第3大的元素,就是4,
如果flag=4:
l_list=[3,2,1]
r_list=[6,5]
因為第3大的元素,r_list長度為2,自然flag就是第3大的元素了,return flag,len(r_list)==k-1,就是結束遞歸的基線條件。
如果flag=1:
l_list=[]
r_list=[6,5,4,3,2]
問題就變成了求r_list里面第K大的元素了
如果flag=6:
l_list=[5,4,3,2,1]
r_list=[]
相當于求l_list里第k-(len(test_list)-len(r_list)+1)大的元素了,這里就是相當于求l_list=[5,4,3,2,1]第2大的元素
通過這三種情況進行遞歸,最終返回flag就是目標元素
最差復雜度就是n+n-1+n-2+n-3+......+1=(1+n)n/2,就是O(n²)
當時我就會回答出了最差復雜度肯定是n²啊,面試小哥說平均復雜度,我說計算平均復雜度好像很復雜吧?感覺他也有點蒙,就說每次都是二分的情況的復雜度,
當時竟然回答了個logn*logn。。。最后還是被面試管提示的。。。太尷尬了。。。
實際上如果每次剛好二分,第一次取flag比較次數是n,第二次是n/2,依次下去是n/4,n/8.....n/2
就是n+n/2+n/4....
最最丟人的是計算這個結果還想了一會。。。看樣該做點高中上數學了。。。
實際結果自然是n(1+1/2+1/4+1/8+....1/2ⁿ)=2n,復雜度自然就是O(n)了
最后實現代碼如下:
#給定一個無序列表,求出第K大的元素,要求復雜度O(n)def find_k(test_list,k): flag=test_list[0] test_list.pop(0) l_list=[i for i in test_list if i < flag] r_list=[i for i in test_list if i >= flag] #結果遞歸的基線條件 if len(r_list)==k-1: return flag elif len(r_list)>k-1: return find_k(r_list,k) else: #因為test_list.pop(0)讓test_list少了一個元素,所以下面需要+1 gap=len(test_list)-len(l_list)+1 k=k-gap return find_k(l_list,k) if __name__ == ’__main__’: test_list = [5, 4, 3, 2, 1,10,20,100] res=find_k(test_list,1) print(res)
補充知識:從N個數選取k個數的組合--不降原則(DFS)
原理 :不降原則(看代碼前先看一下原理吧)
舉個例子:
比如說在6里面隨便選5個數,那么選法都是什么呢?
瞎枚舉?
1234512346
前兩個還不會弄混
然后很可能就亂了
少點數可能不會亂
但是多了就不好整了
比如說在100里隨便選50個數。
1 2 3 4 5 6 7 8 9 10 11 12…
所以我們可以運用不降原則:
保證枚舉的這些數是升序排列
其實真正的不降原則還可以平
比如 1 2 2 3 3 4…
但是這里要說的“不降原則”不能平哦!
對于這道題也不能平
否則就有重復數字了
拿6個里面選3個舉例子
1 2 31 2 41 2 51 2 6
第一輪枚舉完畢。
第二個數加一
1 3 ?
這個“?”應該是4,因為是升序排列
1 3 41 3 51 3 6
接著,就是這樣
1 4 51 4 61 5 6
第一位是1枚舉完畢
第一位是2呢?
2 3 42 3 52 3 62 4 52 4 62 5 6
就是這樣的,枚舉十分清晰,對嗎?
以此類推…
3 4 53 4 63 5 64 5 6
然后就枚舉不了了,結束。
所以說,這樣就可以避免判重了。
代碼
#include<iostream>#include<cstring>using namespace std;int n,k; //全局變量:從n個數的集合中選取k個數int a[25]; //存放n個數的集合數據int vis[25];//在dfs中記錄數據是否被訪問過int re[25];//存放被選取的數字void dfs(int step,int start)//參數step代表選取第幾個數字,參數start代表從集合的第幾個開始選{ if(step==k)//如果選夠了k個就輸出 { for(int i=0;i<k;i++) { cout<<re[i]<<' '; } cout<<endl; } for(int i=start;i<n;i++)//不降原則的核心步驟1:從第i+1個開始選取數字(避免重選) { if(vis[i]==1) continue; vis[i]=1; re[step]=a[i]; dfs(step+1,i+1); //不降原則的核心步驟2:從第i+1個開始選取數字(避免重選) vis[i]=0; } return;}int main(){ while(cin>>n>>k) { memset(a,0,sizeof(a)); memset(re,0,sizeof(re)); memset(vis,0,sizeof(vis)); for(int i=0;i<n;i++) { cin>>a[i]; } dfs(0,0); } return 0;}
運行結果
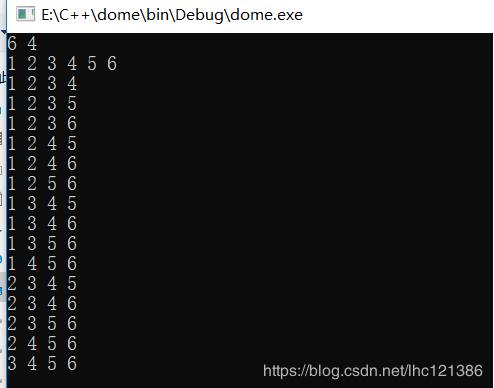
變形——從N個數中選取k個數求和(舉一反三)
代碼
#include<iostream>#include<cstring>using namespace std;int n,k; //全局變量:從n個數的集合中選取k個數int a[25]; //存放n個數的集合數據int vis[25];//在dfs中記錄數據是否被訪問過int re[25];//存放被選取的數字void dfs(int step,int sum,int start)//參數step代表選取第幾個數字,參數sum代表從選取前step-1個數時的總數,參數start代表從集合的第幾個開始選{ if(step==k)//如果選夠了k個就輸出 { cout<<re[0]; for(int i=1;i<k;i++) { cout<<’+’<<re[i]; } cout<<’=’<<sum<<endl; } for(int i=start;i<n;i++)//不降原則的核心步驟1:從第i+1個開始選取數字(避免重選) { if(vis[i]==1) continue; vis[i]=1; re[step]=a[i]; dfs(step+1,sum+a[i],i+1); //不降原則的核心步驟2:從第i+1個開始選取數字(避免重選) vis[i]=0; } return;}int main(){ while(cin>>n>>k) { memset(a,0,sizeof(a)); memset(re,0,sizeof(re)); memset(vis,0,sizeof(vis)); for(int i=0;i<n;i++) { cin>>a[i]; } dfs(0,0,0); } return 0;}
運行結果
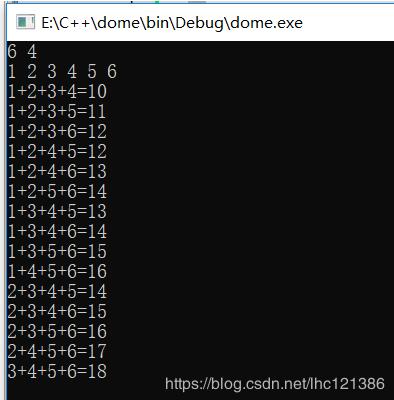
變形——從N個數中選取k個數求積(舉一反三)
代碼
#include<iostream>#include<cstring>using namespace std;int n,k; //全局變量:從n個數的集合中選取k個數int a[25]; //存放n個數的集合數據int vis[25];//在dfs中記錄數據是否被訪問過int re[25];//存放被選取的數字void dfs(int step,int sum,int start)//參數step代表選取第幾個數字,參數start代表從集合的第幾個開始選{ if(step==k)//如果選夠了k個就輸出 { cout<<re[0]; for(int i=1;i<k;i++) { cout<<’*’<<re[i]; } cout<<’=’<<sum<<endl; } for(int i=start;i<n;i++)//不降原則的核心步驟1:從第i+1個開始選取數字(避免重選) { if(vis[i]==1) continue; vis[i]=1; re[step]=a[i]; dfs(step+1,sum*a[i],i+1); //不降原則的核心步驟2:從第i+1個開始選取數字(避免重選) vis[i]=0; } return;}int main(){ while(cin>>n>>k) { memset(a,0,sizeof(a)); memset(re,0,sizeof(re)); memset(vis,0,sizeof(vis)); for(int i=0;i<n;i++) { cin>>a[i]; } dfs(0,1,0); } return 0;}
運行結果

以上這篇Python要求O(n)復雜度求無序列表中第K的大元素實例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。
相關文章:
1. 將properties文件的配置設置為整個Web應用的全局變量實現方法2. docker compose idea CreateProcess error=2 系統找不到指定的文件的問題3. 在Vue 中獲取下拉框的文本及選項值操作4. JS中的常見數組遍歷案例詳解(forEach, map, filter, sort, reduce, every)5. Python語言規范之Pylint的詳細用法6. python爬蟲利用代理池更換IP的方法步驟7. Vue+express+Socket實現聊天功能8. python中pandas.read_csv()函數的深入講解9. SpringBoot集成SSM、Dubbo、Redis、JSP的案例小結及思路講解10. JS算法題解旋轉數組方法示例
 網公網安備
網公網安備