Python itertools.product方法代碼實例
itertools.product:類似于求多個可迭代對象的笛卡爾積。
使用的形式是:
itertools.product(*iterables, repeat=1),
product(X, repeat=3)等價于product(X, X, X)。
1. 直接使用時:分別生成元組,然后合成一個list
import itertoolsaa = itertools.product([’西藏’,’瀑布’,’湖水’], [’月色’,’星空’])bb = list(aa) #按照順序生成笛卡爾積,repeat默認是1print(bb)

2. 假設設置:repeat=3
random_list = list(itertools.product([’西藏’,’瀑布’,’湖水’], [’月色’,’星空’], repeat=3))print(random_list) #此list長度為216
為什么會是216呢?
首先,在不設置 repeat 參數(shù)的時候,默認是1,生成的list長度時6 —— 這可以用數(shù)學的排列組合來表示,從第一個參數(shù)[’西藏’,’瀑布’,’湖水’]取出一個值,有3種可能;從第二個參數(shù)[’月色’,’星空’]取出一個值,有2種可能;故 3*2=6種結果。
然后,當設置 repeat=3 時,也就是說將 repeat=1(默認)的結果再重復2次后(也就是最后一共有3套一樣的第一層結果)再進行排列組合,從第一個結果(6種結果)取出一個元素的可能有6種,同理,從第二第三個重復結果中取出一個元素的可能各有6種,于是它們的組合就有6*6*6=216種。

當然,也是先合成一個元組再組成list的。
3. 所以也能理解下面的結果是27種了吧
random_list = list(itertools.product([’西藏’,’瀑布’,’湖水’], repeat=3))print(random_list)
因為第一層結果是3種可能;執(zhí)行該操作3次,就形成了第一層的3套一樣的結果(每個結果各有3種可能),然后再排列組合就是 3*3*3=27種結果。
4. 如果要從列表中隨機取出幾個不重復的元素的話(原來的列表本身元素不重復),可用 random.sample 方法。
import randomrandom.seed(1) #設置隨機數(shù)種子,可用來檢測相同的隨機數(shù)得到的結果是否一致n = 2aa = random.sample(random_list, n) #隨機列表中的n個元素print(aa)
也就是從上述27種結果中,隨機取出2種,得到:
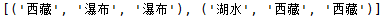
5. 此方法可以用于生成隨機的坐標
random_list = list(itertools.product(range(1,4), range(1,2)))print(random_list)n = 2aa = random.sample(random_list, n) #隨機列表中的n個元素print(aa)
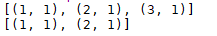
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持好吧啦網。
相關文章:

 網公網安備
網公網安備