python實現(xiàn)logistic分類算法代碼
最近在看吳恩達(dá)的機(jī)器學(xué)習(xí)課程,自己用python實現(xiàn)了其中的logistic算法,并用梯度下降獲取最優(yōu)值。
logistic分類是一個二分類問題,而我們的線性回歸函數(shù)
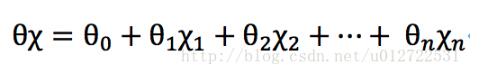
的取值在負(fù)無窮到正無窮之間,對于分類問題而言,我們希望假設(shè)函數(shù)的取值在0~1之間,因此logistic函數(shù)的假設(shè)函數(shù)需要改造一下
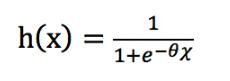
由上面的公式可以看出,0 < h(x) < 1,這樣,我們可以以1/2為分界線
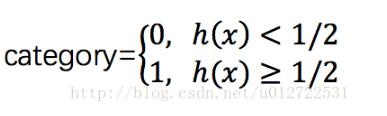
cost function可以這樣定義
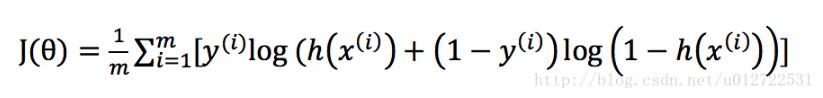
其中,m是樣本的數(shù)量,初始時θ可以隨機(jī)給定一個初始值,算出一個初始的J(θ)值,再執(zhí)行梯度下降算法迭代,直到達(dá)到最優(yōu)值,我們知道,迭代的公式主要是每次減少一個偏導(dǎo)量
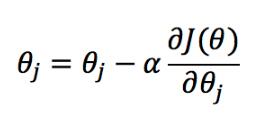
如果將J(θ)代入化簡之后,我們發(fā)現(xiàn)可以得到和線性回歸相同的迭代函數(shù)
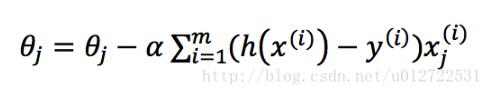
按照這個迭代函數(shù)不斷調(diào)整θ的值,直到兩次J(θ)的值差值不超過某個極小的值之后,即認(rèn)為已經(jīng)達(dá)到最優(yōu)解,這其實只是一個相對較優(yōu)的解,并不是真正的最優(yōu)解。 其中,α是學(xué)習(xí)速率,學(xué)習(xí)速率越大,就能越快達(dá)到最優(yōu)解,但是學(xué)習(xí)速率過大可能會讓懲罰函數(shù)最終無法收斂,整個過程python的實現(xiàn)如下
import mathALPHA = 0.3DIFF = 0.00001def predict(theta, data): results = [] for i in range(0, data.__len__()): temp = 0 for j in range(1, theta.__len__()): temp += theta[j] * data[i][j - 1] temp = 1 / (1 + math.e ** (-1 * (temp + theta[0]))) results.append(temp) return resultsdef training(training_data): size = training_data.__len__() dimension = training_data[0].__len__() hxs = [] theta = [] for i in range(0, dimension): theta.append(1) initial = 0 for i in range(0, size): hx = theta[0] for j in range(1, dimension): hx += theta[j] * training_data[i][j] hx = 1 / (1 + math.e ** (-1 * hx)) hxs.append(hx) initial += (-1 * (training_data[i][0] * math.log(hx) + (1 - training_data[i][0]) * math.log(1 - hx))) initial /= size iteration = initial initial = 0 counts = 1 while abs(iteration - initial) > DIFF: print('第', counts, '次迭代, diff=', abs(iteration - initial)) initial = iteration gap = 0 for j in range(0, size): gap += (hxs[j] - training_data[j][0]) theta[0] = theta[0] - ALPHA * gap / size for i in range(1, dimension): gap = 0 for j in range(0, size):gap += (hxs[j] - training_data[j][0]) * training_data[j][i] theta[i] = theta[i] - ALPHA * gap / size for m in range(0, size):hx = theta[0]for j in range(1, dimension): hx += theta[j] * training_data[i][j]hx = 1 / (1 + math.e ** (-1 * hx))hxs[i] = hxiteration += -1 * (training_data[i][0] * math.log(hx) + (1 - training_data[i][0]) * math.log(1 - hx)) iteration /= size counts += 1 print(’training done,theta=’, theta) return thetaif __name__ == ’__main__’: training_data = [[1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 0, 0], [1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 1], [0, 1, 0, 0, 0, 1],[0, 0, 0, 0, 1, 1]] test_data = [[0, 1, 0, 0, 0], [0, 0, 0, 0, 1]] theta = training(training_data) res = predict(theta, test_data) print(res)
運(yùn)行結(jié)果如下

以上這篇python實現(xiàn)logistic分類算法代碼就是小編分享給大家的全部內(nèi)容了,希望能給大家一個參考,也希望大家多多支持好吧啦網(wǎng)。
相關(guān)文章:
1. ajax請求添加自定義header參數(shù)代碼2. ASP基礎(chǔ)知識VBScript基本元素講解3. 解決android studio引用遠(yuǎn)程倉庫下載慢(JCenter下載慢)4. Kotlin + Flow 實現(xiàn)Android 應(yīng)用初始化任務(wù)啟動庫5. Python requests庫參數(shù)提交的注意事項總結(jié)6. Gitlab CI-CD自動化部署SpringBoot項目的方法步驟7. 利用CSS3新特性創(chuàng)建透明邊框三角8. 淺談SpringMVC jsp前臺獲取參數(shù)的方式 EL表達(dá)式9. axios和ajax的區(qū)別點總結(jié)10. python操作mysql、excel、pdf的示例

 網(wǎng)公網(wǎng)安備
網(wǎng)公網(wǎng)安備