目錄一、算法概述二、算法步驟三、相關(guān)概念四、算法優(yōu)缺點(diǎn)五、算法實(shí)現(xiàn)六、算法優(yōu)化一、算法概述 主成分分析 （Principal ComponentAnalysis，PCA）是一種掌握事物主要矛盾的統(tǒng)計(jì)分析方法，它可以從多元事物中解析出主要影響因素，揭示事物的本質(zhì)，簡化復(fù)雜的問題。 PCA 是最常用的一種降維方法，它的目標(biāo)是通過某種線性投影，將高維的數(shù)據(jù)映射到低維的空間中，并期望在所投影的維度上數(shù)據(jù)的方差最大，以此使用較少的維度，同時保留較多原數(shù)據(jù)的維度。 PCA 算法目標(biāo)是求出樣本數(shù)據(jù)協(xié)方差矩陣的特征值和特征向量，而協(xié)方差矩陣的特征向量的方向就是PCA需要投影的方向。使樣本數(shù)據(jù)向低維投影后，能盡可能表征原始的數(shù)據(jù)。 PCA 可以把具有相關(guān)性的高維變量合成為線性無關(guān)的低維變量，稱為主成分。主成分能夠盡可能的保留原始數(shù)據(jù)的信息。 PCA 通常用于高維數(shù)據(jù)集的探索與可視化，還可以用作數(shù)據(jù)壓縮和預(yù)處理等。二、算法步驟

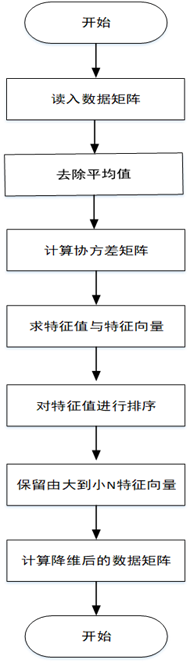
1.將原始數(shù)據(jù)按行組成m行n列的矩陣X

2.將X的每一列（代表一個屬性字段）進(jìn)行零均值化，即減去這一列的均值

3.求出協(xié)方差矩陣

4.求出協(xié)方差矩陣的特征值及對應(yīng)的特征向量r

5.將特征向量按對應(yīng)特征值大小從左到右按列排列成矩陣，取前k列組成矩陣P

6.計(jì)算降維到k維的數(shù)據(jù)

三、相關(guān)概念 方差：描述一個數(shù)據(jù)的離散程度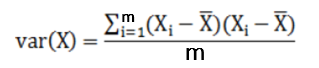

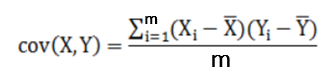
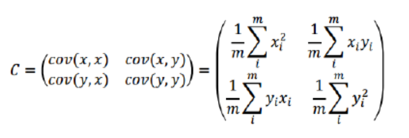
協(xié)方差：描述兩個數(shù)據(jù)的相關(guān)性，接近1就是正相關(guān)，接近-1就是負(fù)相關(guān)，接近0就是不相關(guān)

協(xié)方差矩陣：協(xié)方差矩陣是一個對稱的矩陣，而且對角線是各個維度的方差

特征值：用于選取降維的K個特征值 特征向量：用于選取降維的K個特征向量四、算法優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

僅僅需要以方差衡量信息量，不受數(shù)據(jù)集以外的因素影響。 各主成分之間正交，可消除原始數(shù)據(jù)成分間的相互影響的因素。 計(jì)算方法簡單，主要運(yùn)算是特征值分解，易于實(shí)現(xiàn)。

缺點(diǎn)

主成分各個特征維度的含義具有一定的模糊性，不如原始樣本特征的解釋性強(qiáng)。 方差小的非主成分也可能含有對樣本差異的重要信息，降維丟棄的數(shù)據(jù)可能對后續(xù)數(shù)據(jù)處理有影響。五、算法實(shí)現(xiàn)

自定義實(shí)現(xiàn)

import numpy as np# 對初始數(shù)據(jù)進(jìn)行零均值化處理def zeroMean(dataMat): # 求列均值 meanVal = np.mean(dataMat, axis=0) # 求列差值 newData = dataMat - meanVal return newData, meanVal# 對初始數(shù)據(jù)進(jìn)行降維處理def pca(dataMat, percent=0.19): newData, meanVal = zeroMean(dataMat) # 求協(xié)方差矩陣 covMat = np.cov(newData, rowvar=0) # 求特征值和特征向量 eigVals, eigVects = np.linalg.eig(np.mat(covMat)) # 抽取前n個特征向量 n = percentage2n(eigVals, percent) print('數(shù)據(jù)降低到：' + str(n) + ’維’) # 將特征值按從小到大排序 eigValIndice = np.argsort(eigVals) # 取最大的n個特征值的下標(biāo) n_eigValIndice = eigValIndice[-1:-(n + 1):-1] # 取最大的n個特征值的特征向量 n_eigVect = eigVects[:, n_eigValIndice] # 取得降低到n維的數(shù)據(jù) lowDataMat = newData * n_eigVect reconMat = (lowDataMat * n_eigVect.T) + meanVal return reconMat, lowDataMat, n# 通過方差百分比確定抽取的特征向量的個數(shù)def percentage2n(eigVals, percentage): # 按降序排序 sortArray = np.sort(eigVals)[-1::-1] # 求和 arraySum = sum(sortArray) tempSum = 0 num = 0 for i in sortArray:tempSum += inum += 1if tempSum >= arraySum * percentage: return numif __name__ == ’__main__’: # 初始化原始數(shù)據(jù)(行代表樣本,列代表維度) data = np.random.randint(1, 20, size=(6, 8)) print(data) # 對數(shù)據(jù)降維處理 fin = pca(data, 0.9) mat = fin[1] print(mat)

利用Sklearn庫實(shí)現(xiàn)

import matplotlib.pyplot as pltfrom sklearn.decomposition import PCAfrom sklearn.datasets import load_iris# 加載數(shù)據(jù)data = load_iris()x = data.datay = data.target# 設(shè)置數(shù)據(jù)集要降低的維度pca = PCA(n_components=2)# 進(jìn)行數(shù)據(jù)降維reduced_x = pca.fit_transform(x)red_x, red_y = [], []green_x, green_y = [], []blue_x, blue_y = [], []# 對數(shù)據(jù)集進(jìn)行分類for i in range(len(reduced_x)): if y[i] == 0:red_x.append(reduced_x[i][0])red_y.append(reduced_x[i][1]) elif y[i] == 1:green_x.append(reduced_x[i][0])green_y.append(reduced_x[i][1]) else:blue_x.append(reduced_x[i][0])blue_y.append(reduced_x[i][1])plt.scatter(red_x, red_y, c=’r’, marker=’x’)plt.scatter(green_x, green_y, c=’g’, marker=’D’)plt.scatter(blue_x, blue_y, c=’b’, marker=’.’)plt.show()六、算法優(yōu)化

PCA是一種線性特征提取算法，通過計(jì)算將一組特征按重要性從小到大重新排列得到一組互不相關(guān)的新特征，但該算法在構(gòu)造子集的過程中采用等權(quán)重的方式，忽略了不同屬性對分類的貢獻(xiàn)是不同的。

KPCA算法

KPCA是一種改進(jìn)的PCA非線性降維算法，它利用核函數(shù)的思想，把樣本數(shù)據(jù)進(jìn)行非線性變換，然后在變換空間進(jìn)行PCA，這樣就實(shí)現(xiàn)了非線性PCA。

局部PCA算法

局部PCA是一種改進(jìn)的PCA局部降維算法，它在尋找主成分時加入一項(xiàng)具有局部光滑性的正則項(xiàng)，從而使主成分保留更多的局部性信息。

到此這篇關(guān)于Python機(jī)器學(xué)習(xí)之PCA降維算法詳解的文章就介紹到這了,更多相關(guān)Python PCA降維算法內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！